How to get last line in cell in Excel
To get the last word from a text string, you can use a formula based on the TRIM, SUBSTITUTE, RIGHT, and REPT functions.
Formula
=TRIM(RIGHT(SUBSTITUTE(B5,CHAR(10),REPT(" ",200)),200))
Note: 200 is an arbitrary number that represents the longest line you expect to find in a cell. If you have longer lines, increase this number as needed.
Explanation
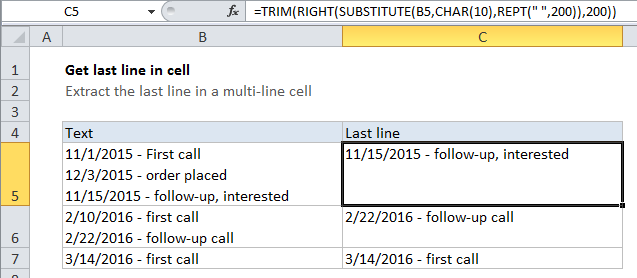
In the example shown, the formula in C5 is:
=TRIM(RIGHT(SUBSTITUTE(B5,CHAR(10),REPT(" ",200)),200))
How this formula works
This formula takes advantage of the fact that TRIM will remove any number of leading spaces. We look for line breaks and “flood” the text with spaces where we find one. Then we come back and grab text from the right.
Working from the inside out, we use the SUBSTITUTE function to find all line breaks (char 10) in the text, and replace each one with 200 spaces:
SUBSTITUTE(B5,CHAR(10),REPT(" ",200))
After the substitution, the looks like this (with hyphens marking spaces for readability):
line one----------line two----------line three
With 200 spaces between each line of text.
Next, the RIGHT function extracts 200 characters, starting from the right. The result will look like this:
-------line three
Finally, the TRIM function removes all leading spaces, and returns the last line.