NORM.DIST function: Description, Usage, Syntax, Examples and Explanation
What is NORM.DIST function in Excel?
Syntax of NORM.DIST function
NORM.DIST(x,mean,standard_dev,cumulative)
The NORM.DIST function syntax has the following arguments:
- X Required. The value for which you want the distribution.
- Mean Required. The arithmetic mean of the distribution.
- Standard_dev Required. The standard deviation of the distribution.
- Cumulative Required. A logical value that determines the form of the function. If cumulative is TRUE, NORM.DIST returns the cumulative distribution function; if FALSE, it returns the probability density function.
NORM.DIST formula explanation
- If mean or standard_dev is nonnumeric, NORM.DIST returns the #VALUE! error value.
- If standard_dev ≤ 0, NORM.DIST returns the #NUM! error value.
- If mean = 0, standard_dev = 1, and cumulative = TRUE, NORM.DIST returns the standard normal distribution, NORM.S.DIST.
- The equation for the normal density function (cumulative = FALSE) is:
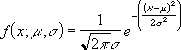
- When cumulative = TRUE, the formula is the integral from negative infinity to x of the given formula.
Example of NORM.DIST function
Steps to follow:
1. Open a new Excel worksheet.
2. Copy data in the following table below and paste it in cell A1
Note: For formulas to show results, select them, press F2 key on your keyboard and then press Enter.
You can adjust the column widths to see all the data, if need be.
| Data | Description | |
| 42 | Value for which you want the distribution | |
| 40 | Arithmetic mean of the distribution | |
| 1.5 | Standard deviation of the distribution | |
| Formula | Description | Result |
| =NORM.DIST(A2,A3,A4,TRUE) | Cumulative distribution function for the terms above | 0.9087888 |
| =NORM.DIST(A2,A3,A4,FALSE) | Probability mass function for the terms above | 0.10934 |