Sales Calculator in Excel
Below we will look at a program in Excel VBA that calculates the total sales of each employee over a period of three years.
Situation:
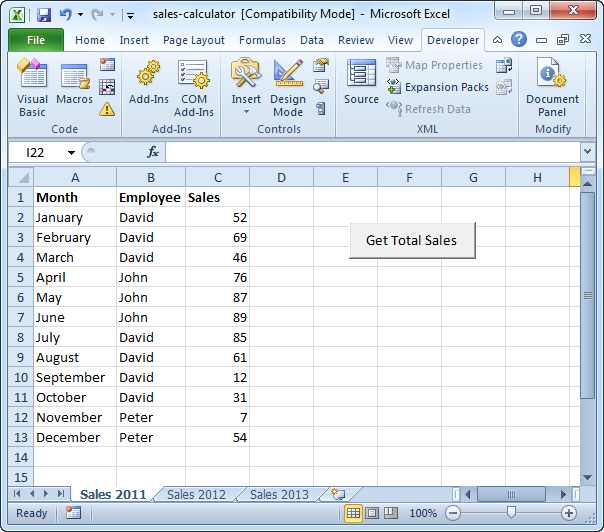
The other two sheets have the same setup, but with different combinations of months and employees, and different sales numbers. There are several ways to calculate the total sales of each employee in Excel, but we will see that it can be done in Excel VBA very easily.
Place a command button on your worksheet and add the following code lines:
1. First, we declare three variables and one Worksheet object. One variable of type String we call employee, one variable of type Integer we call total, one Worksheet object we call sheet, and one variable of type Integer we call i.
Dim employee As String, total As Integer, sheet As Worksheet, i As Integer.
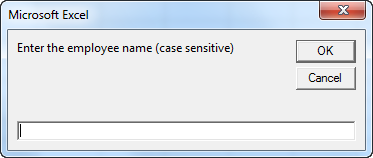
2. We initialize two variables. We initialize the variable total with value 0. We use the InputBox function to get the employee name from the user.
total = 0
employee = InputBox
(“Enter the employee name (case sensitive)”)
3. After the user has entered an employee name, we want to calculate the total sales of this employee. The workbook consists of three sheets. We want a program that can still be used if sheets are added in the future. Therefore we use the following code line:
4. We start another For Next loop.
5. If the entered employee name matches with the employee name in column B, Excel VBA adds the sales number to the variable total. Add the following code lines:
If sheet.Cells(i, 2).Value = employee Then
total = total + sheet.Cells(i, 3).Value
End If6. Don’t forget to close both loops.
Next sheet
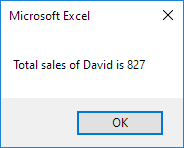
7. Finally, we display the total sales of the employee using a msgbox.
8. Test the program.
Result for David: