Get day from date in Excel

This tutorial show how to Get day from date in Excel using the example below.

If you need to extract the day from a date, you can use the DAY function.

Formula

=DAY(date)

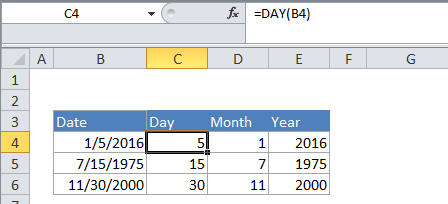
Explanation of how this formula works

In the generic form of the formula above, the date must be in a form that Excel recognizes as a valid date.

Here’s how the formula works:

The DAY function takes just one argument, the date from which you want to extract the day. In the example, the formula is:

=DAY(B4)

B4 contains a date value for January 5, 2016. The DAY function returns the number 5 representing the day component of the date.

Note that you can use DAY to extract the day from a day entered as text:

=DAY("1/5/2016")

But this can produce unpredictable results on computers using different regional date settings. In general it’s better (and more flexible) to supply an address to a cell that already contains a valid date value as the argument for DAY.