CONFIDENCE.NORM function: Description, Usage, Syntax, Examples and Explanation

by

What is CONFIDENCE.NORM function in Excel?

CONFIDENCE.NORM function is one of Statistical functions in Microsoft Excel that returns the confidence interval for a population mean, using a normal distribution.
The confidence interval is a range of values. Your sample mean, x, is at the center of this range and the range is x ± CONFIDENCE.NORM. For example, if x is the sample mean of delivery times for products ordered through the mail, x ± CONFIDENCE.NORM is a range of population means. For any population mean, μ0, in this range, the probability of obtaining a sample mean further from μ0 than x is greater than alpha; for any population mean, μ0, not in this range, the probability of obtaining a sample mean further from μ0 than x is less than alpha. In other words, assume that we use x, standard_dev, and size to construct a two-tailed test at significance level alpha of the hypothesis that the population mean is μ0. Then we will not reject that hypothesis if μ0 is in the confidence interval and will reject that hypothesis if μ0 is not in the confidence interval. The confidence interval does not allow us to infer that there is probability 1 – alpha that our next package will take a delivery time that is in the confidence interval.

Syntax of CONFIDENCE.NORM function

CONFIDENCE.NORM(alpha,standard_dev,size)

The CONFIDENCE.NORM function syntax has the following arguments:

  • Alpha     Required. The significance level used to compute the confidence level. The confidence level equals 100*(1 – alpha)%, or in other words, an alpha of 0.05 indicates a 95 percent confidence level.
  • Standard_dev     Required. The population standard deviation for the data range and is assumed to be known.
  • Size     Required. The sample size.

CONFIDENCE.NORM formula explanation

  • If any argument is nonnumeric, CONFIDENCE.NORM returns the #VALUE! error value.
  • If alpha ≤ 0 or alpha ≥ 1, CONFIDENCE.NORM returns the #NUM! error value.
  • If standard_dev ≤ 0, CONFIDENCE.NORM returns the #NUM! error value.
  • If size is not an integer, it is truncated.
  • If size < 1, CONFIDENCE.NORM returns the #NUM! error value.
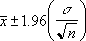
  • If we assume alpha equals 0.05, we need to calculate the area under the standard normal curve that equals (1 – alpha), or 95 percent. This value is ± 1.96. The confidence interval is therefore:Equation

Example of CONFIDENCE.NORM function

Steps to follow:

1. Open a new Excel worksheet.

2. Copy data in the following table below and paste it in cell A1

Note: For formulas to show results, select them, press F2 key on your keyboard and then press Enter.

You can adjust the column widths to see all the data, if need be.

Data Description
0.05 Significance level
2.5 Standard deviation of the population
50 Sample size
Formula Description Result
=CONFIDENCE.NORM(A2,A3,A4) Confidence interval for a population mean. In other words, the confidence interval for the underlying population mean for travel to work equals 30 ± 0.692952 minutes, or 29.3 to 30.7 minutes. 0.692952

Leave a Reply

Your email address will not be published.